Chapter 3 Generalized Linear Models
Generalized Linear Models (GLM) are an extension of linear models that can deal with non-normal distributions of the response variable, providing an alternative way to transform the response. The distributions used include those like Poisson, binomial, negative binomial, and gamma.
GLM generalizes linear regression by allowing the linear model to be related to the response variable through a link function and allowing the magnitude of the variance of each measurement to be a function of its predicted value. GLM were formulated by John Nelder and Robert Wedderburn as a way to unify several statistical models, including linear regression, logistic regression, and Poisson regression.
For the development of this course we will focus on the calibration of binary logistic and Poisson regression models, although most of the contents are extrapolable to the different types of regression within GLM.
A generalized linear model has three basic components:
Random component: Identical the response variable and its probability distribution.
Systematic component: Specifies the explanatory variables (independent or predictor) used in the linear predictive function.
Link function: is a function of the expected value of \(Y, E(Y)\), as a linear combination of predictive variables.
3.1 Logistic regression
The primary objective of logistic regression is to model how the probability of occurrence of an event, usually dichotomous, is influenced by the presence of various factors10. Logistic regression models are regression models that allow us to study whether or not a binomial variable depends on another variable(s).
To calibrate a logistic regression model we classify the value of the dependent variable as 0 when an event does not occur and with 1 when it is present, and we try to quantify the possible relationship between that event and some independent variable(s). The value returned or predicted by the regression model is the probability associated with the occurrence of that event.
Therefore, the logistic regression models the probability of a binomial process as the logistic function of a linear combination of the independent variable(s), being a particular case of regression where the dependent variable is categorical. The technique does not impose as strong constraints on the distribution of errors as in the case of linear or Gaussian models. In fact, the only assumption is the linear independece of the predictors.
The estimation of regression coefficients is done from the data using a maximum likelihood approach rather than the ordinary least squares. Similar to linear regression, logistic regression:
Evaluates/fits explanatory models.
Estimates the significance level of the predictors.
Allows to conduct predictions.
The model is generally presented in the following format, where \(\beta\) refers to the parameters (or coefficients) and \(X\) represents the independent variables:
\[log(P)=\beta_0+\beta_nX_n\]
The \(log(P)\), or log-odds ratio, is defined by \(ln[p/(1-p)]\) and expresses the natural logarithm of the ratio between the probability that an event will occur, \(P(Y=1)\), to the probability that it will not occur. We are usually concerned with the predicted probability of an event occuring and that is defined by:
\[P=\frac{1}{1+exp^{-z}}\] where:
\[z=\beta_0+\beta_nX_n\]
The function of R that allows to adjust GLM models is glm(). Same as linear regression, glm() requires an argument that describes the variables that are going to intervene in the process (formula), and a data.frame containing the values of the dependent and independent variables. However, it requires an additional argument that specify the type of distribution that we are going to use (family).
As stated in the help for this function the only difference from linear regression is the obligation to specify the type of error distribution that we want to use. Let’s fit a example model. We will use data from the logit.csv file (Table 3.1) which contains data on forest fire occurrence in Spain from 1988 to 2008:
Figure 3.1: Structure of the logit.csv file.
str(logit)## 'data.frame': 3582 obs. of 12 variables:
## $ logit_1_0 : int 1 1 1 1 1 1 1 1 1 1 ...
## $ Cattle : num 480 763 496 2666 271 ...
## $ Prot_area : num 24031 1000000 313823 0 609512 ...
## $ Powerlines: num 0 0 261510 0 0 ...
## $ Railroads : num 0 0 0 0 0 0 0 0 0 0 ...
## $ WAI : num 0 452471 344277 430075 341357 ...
## $ WGI : int 0 0 150339 200063 0 0 0 0 0 0 ...
## $ WUI : int 0 0 0 0 0 0 0 0 0 0 ...
## $ Machinery : num 0.33 2.17 0.51 0.83 2.86 ...
## $ FAPU : num 0 0 0 0 0 ...
## $ Tracks : num 0 0 0 74735 15167 ...
## $ Change_pop: num -0.006 -0.075 0.2 0.148 0.241 ...Where:
- logit_1_0: is the dependent variable, 1-fire and 0-no fire.
- Cattle: is the amount of ovine cattle individuals.
- Prot_area: is the area (in m^2) covered by natural protection figures.
- Powerlines: is the area covered by a 200 m buffer from power lines over forest areas.
- Railroads: is the area (in m^2) covered by a 200 m buffer from railroads over forest areas.
- WAI: or Wildland-Agricultural interface is the area (in m^2) covered by a 200 m buffer from the boundary between forest and croplands over forest areas.
- WGI: or Wildland-Grassland interface is the area (in m^2) covered by a 200 m buffer from the boundary between forest and grasslands over forest areas.
- WUI: or Wildland-Agricultural interface is the area (in m^2) covered by a 200 m buffer from the boundary between forest and urban settelments over forest areas.
- Machinery: density of agricultural machinery.
- FAPU: area of forest areas under public management.
- Tracks: is the area (in m^2) covered by a 200 m buffer from tracks over forest areas.
- Change_pop: relative change in population from 1990 to 2010.
All predictors are expected to show a positive relationship, ie, the higher the value, the higher the predicted probability of fire occurrence; with the only exception of Prot_area. For a more detailed description see @Rodrigues2014.
So, let’s go and fit our first logit model. We have everything we need except the kid of family we have to use in the case of a logistic model which is binomial.
mod.logit<-glm(logit_1_0 ~ ., data = logit, family = binomial)
summary(mod.logit)##
## Call:
## glm(formula = logit_1_0 ~ ., family = binomial, data = logit)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -5.2314 -0.6086 -0.4270 0.2706 2.6884
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.528e+00 9.995e-02 -15.290 < 2e-16 ***
## Cattle 1.114e-05 9.975e-06 1.117 0.26407
## Prot_area -1.502e-07 1.335e-07 -1.125 0.26056
## Powerlines 2.070e-06 1.299e-06 1.593 0.11113
## Railroads 1.900e-06 5.890e-07 3.226 0.00125 **
## WAI 1.466e-05 5.627e-07 26.060 < 2e-16 ***
## WGI -1.567e-06 2.404e-07 -6.520 7.02e-11 ***
## WUI 2.698e-06 1.058e-06 2.550 0.01078 *
## Machinery -2.646e-02 1.796e-02 -1.474 0.14059
## FAPU 3.445e-07 1.887e-07 1.825 0.06794 .
## Tracks 8.281e-07 3.520e-07 2.353 0.01863 *
## Change_pop -2.010e+00 3.959e-01 -5.077 3.84e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 4852.9 on 3581 degrees of freedom
## Residual deviance: 2534.2 on 3570 degrees of freedom
## AIC: 2558.2
##
## Number of Fisher Scoring iterations: 6And there it is. The output from summary() also looks familiar, doesn’t it? The main difference is that we do not obtain standard errors or *R2. Instead of that we have the AIC (Akaike Information Criterion) that measures the amount of information lost by a model. It has no straight interpretation as is the case of the R2. It suffices to know that the lesser the AIC the lesser the information lost and, thus, the better the model. Anything else (Estimates,Pr(>|z|)) remains the same. However, take into account that we are not predicting the actual value of a dependent variable but the likehood or chance of an event to happen. Therefore, the higher the coefficient the higher the chance to happen and viceversa.
3.1.1 Making predictions from our logit model
Essentially this works in the same way we saw in the linear regression:
mod.logit.pred<-predict(mod.logit, logit, type = 'response')
hist(mod.logit.pred, col='steelblue',breaks = 15, xlab = 'Predicted probability')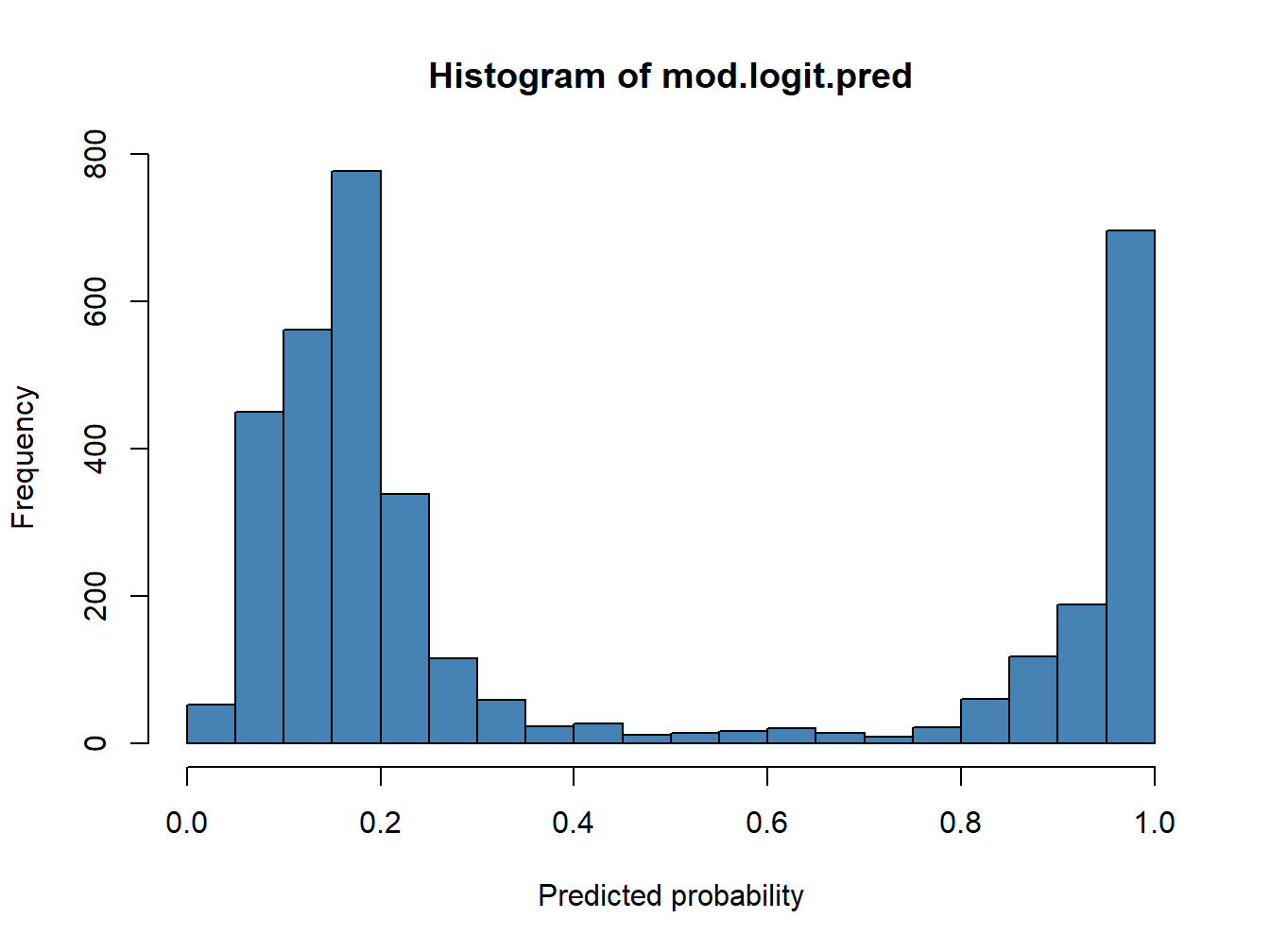
The main difference respect to what we saw in linear regression is that here our response variable is categorical, either 1 or 0. Consequently, we cannot evaluate the model performane in the same way. A classical approach here is the use of contingengi tables and measuring the rate success in the classification using a reference threshold.
ctable<-data.frame(cbind(logit$logit_1_0,mod.logit.pred))
names(ctable)<-c("Obs","Pred")
boxplot(Pred~Obs, data=ctable, col=c('darkgreen','darkred'))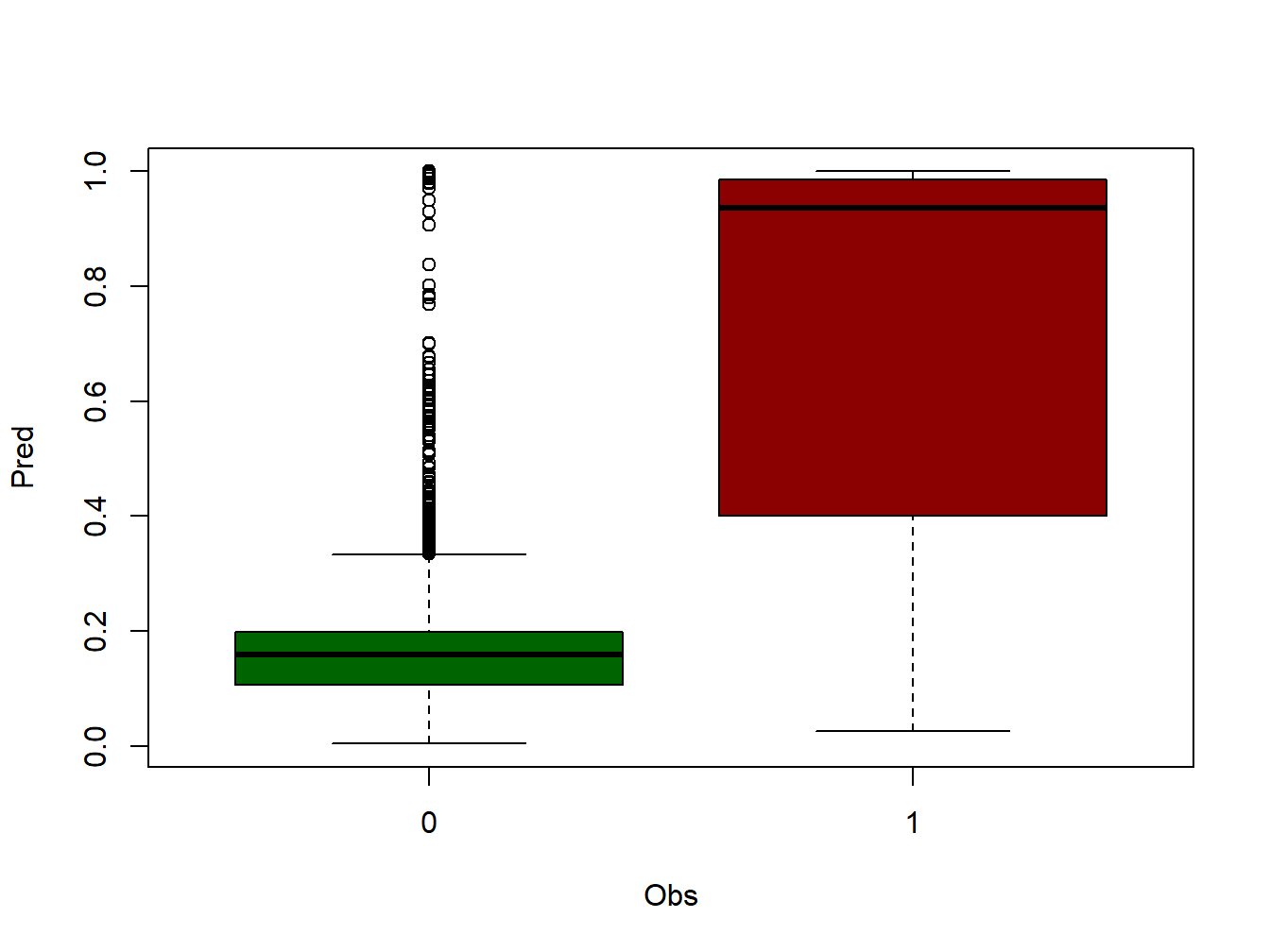
threshold<-0.5
ctable$Pred[ctable$Pred > threshold] <-1
ctable$Pred[ctable$Pred < threshold] <-0- First, we create a table joining our response variable
logit_1_0and the predicted probabilitymod.logit.pred. - Then we rename the headers and build a
boxplotgroupingmod.logit.predaccording to the observed eventlogit_1_0(0-no iire, 1-fire). - At this point we have to determine a threshold to classify the predicted probability. The common approach is us 0.5 and consider 0.5-1.0 as 1 and 0-0.5 as 0.
- Once the threshold is determined we recode the predicted probability into 0 and 1.
The final stepis build the contingency table with table() and calculate the rate o of success by dividing the sum of correctly classified events (diagonal) by the sample size (sum(diag(accuracy))/sum(accuracy)).
accuracy <- table(ctable$Pred, ctable$Obs)
print('Correctly classified:')## [1] "Correctly classified:"sum(diag(accuracy))/sum(accuracy)## [1] 0.8774428| 0 | 1 | |
|---|---|---|
| 0 | 2044 | 375 |
| 1 | 64 | 1099 |
In this case we obtained a 0.88 success rate or what is the same, the model classifies well 88% of the events. Note that this measure of performance or validation is not adequate since we are using the input data. To do it properly we must split the original data into several samples, at least one to calibrate the model and another to conduct the validation.
There are many other measures of performance for glm and logit models but they are kind of specific. In following modules we will cover other options much more refined which are can be applied to any kind of binary model.
EXERCISE 5:
Try to optimize the example from above to drop variables which are not needed (non-significant or collinear) and also minimizing the AIC.
Once you have your final model build the contingency table and create a boxplot.
Deliverables:
- Create a script with the instructions used (.R file ) with the instructions used.
3.2 Poisson regression
Once seen the operation of linear and logistic regression models, we will see another possibility within GLM. Specifically, this is the case of the Poisson regression. These regression models are mainly characterized by using count data as dependent variable.
If we recall the case of Logistic regression, in that regression model the dependent variable was expressed in terms of occurrence (1) or non-occurrence (0) of an event in a given time interval.
In the case of the Poisson regression we will use as a dependent variable the number of times a given event occurs in a given time interval. In statistics, Poisson regression is a type of generalized linear model in which the response variable follows a Poisson distribution and the logarithm of its expected value can be modeled by a linear combination of unknown parameters, ie, the logarithm is the canonical link function.
Let’s look at a simple example of fitting a Poisson regression model using the sample data taken from:
https://stats.idre.ucla.edu/stat/data/poisson_sim.csv
In this example, num_awards is the outcome variable and indicates the number of awards earned by students at a high school in a year, math is a continuous predictor variable and represents students’ scores on their math final exam, and prog is a categorical predictor variable with three levels indicating the type of program in which the students were enrolled. It is coded as 1 = “General”, 2 = “Academic” and 3 = “Vocational”. Let’s start with loading the data and looking at some descriptive statistics.
data<-read.csv('https://stats.idre.ucla.edu/stat/data/poisson_sim.csv')
str(data)## 'data.frame': 200 obs. of 4 variables:
## $ id : int 45 108 15 67 153 51 164 133 2 53 ...
## $ num_awards: int 0 0 0 0 0 0 0 0 0 0 ...
## $ prog : int 3 1 3 3 3 1 3 3 3 3 ...
## $ math : int 41 41 44 42 40 42 46 40 33 46 ...head(data)## id num_awards prog math
## 1 45 0 3 41
## 2 108 0 1 41
## 3 15 0 3 44
## 4 67 0 3 42
## 5 153 0 3 40
## 6 51 0 1 42mod.poisson<-glm(num_awards~math+prog,family=poisson,data=data)
summary(mod.poisson)##
## Call:
## glm(formula = num_awards ~ math + prog, family = poisson, data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1840 -0.9003 -0.5891 0.3948 2.9539
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.578057 0.676823 -8.242 <2e-16 ***
## math 0.086121 0.009586 8.984 <2e-16 ***
## prog 0.123273 0.163261 0.755 0.45
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 287.67 on 199 degrees of freedom
## Residual deviance: 203.45 on 197 degrees of freedom
## AIC: 385.51
##
## Number of Fisher Scoring iterations: 6In this case we use poisson as family the rest is as we have seen before, nothing new. We can obtain predictions, RMSE and work with the AIC to calibrate the model.
Believe it or not, this kind of variable is quite frequent both in nature or environmetal science (species distribution models) or health sciences (disease outbreak).↩